

Next: Factoring
Up: Quantum Computing Notes
Previous: Quantum Computing Notes
Let us assume that we start with the state
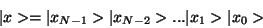 |
(1) |
which is the bit representation of the 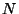 digit number
digit number 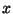 with
with 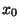 being
th value of the least significant bit, and
being
th value of the least significant bit, and 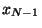 that value of the most
significant bit. Thus
the number
that value of the most
significant bit. Thus
the number 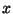 is given by
is given by
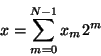 |
(2) |
with the 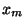 taking the values
taking the values 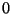 or 1.
We now want to take this state to the state
or 1.
We now want to take this state to the state
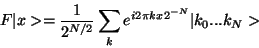 |
(3) |
where 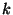 is the number represented by
is the number represented by
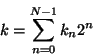 |
(4) |
Note that we have reversed the representation for 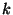 so that the least
significant bit is represented by the first qubit state, and the most
significant is represented by the last qubit state.
so that the least
significant bit is represented by the first qubit state, and the most
significant is represented by the last qubit state.
Now, the phase factor can be rewritten as
since
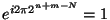 if
if 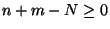 .
We thus notice that the phase for any given value of
.
We thus notice that the phase for any given value of 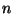 (ie the n-th least
significant bit of k) depends only on the values of the
bits of
(ie the n-th least
significant bit of k) depends only on the values of the
bits of 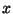 of order less
that
of order less
that 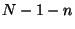 . If we line up the bit representations of
. If we line up the bit representations of 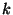 and
and 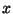 we have
we have
The Fourier factor which depends on 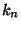 is
is
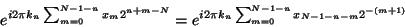 |
(6) |
and depends only on
those bits of the representation of 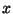 which lie at or to the
right of that bit
in the representation of
which lie at or to the
right of that bit
in the representation of 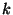 . Furthermore, we note that in the factor which
depends on
. Furthermore, we note that in the factor which
depends on 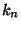 , the phase which depends on the largest
, the phase which depends on the largest 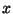 bit, namely
bit, namely
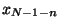 is
is
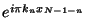 which has only values of plus or minus
1 .
which has only values of plus or minus
1 .
We can now perform the Fourier Transform bit by bit starting with the lowest
digit of 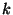 , namely
, namely 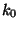 . Let me assume that we have managed to
transform the state
. Let me assume that we have managed to
transform the state 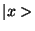 by replacing the
by replacing the 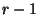 highest digits of
highest digits of 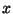 with the
lowest
with the
lowest 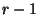 digits of
digits of 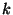 . I.e., I have created, by some sequence of
transformations, the state
. I.e., I have created, by some sequence of
transformations, the state
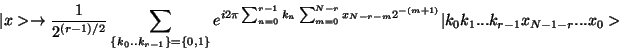 |
(7) |
I now show how to advance this to next stage where we will create the
expression up to the 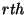 bit. . We can accomplish
this by generating a transformation of the form
bit. . We can accomplish
this by generating a transformation of the form
This transformation can be decomposed into the two sets of transformations
and
The first transformation is just a 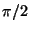 rotation of the
rotation of the 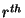 bit.
bit.
The second set just correspond to a series of controlled one bit phase rotations.
I.e., these are transformations which phase rotate the 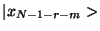 bit
depending on whether
bit
depending on whether 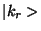 bit is one or zero.
bit is one or zero.
Thus given the transform up to 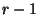 bits, it requires a single
bits, it requires a single 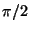 rotation of a single bit, and
rotation of a single bit, and 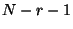 controlled single-bit phase
rotations, for a total of
controlled single-bit phase
rotations, for a total of 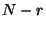 operations.
Thus the whole Fourier transformation requires
operations.
Thus the whole Fourier transformation requires
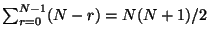 operations
(
operations
(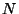 , we recall is the number of bits in each of the numbers).
, we recall is the number of bits in each of the numbers).
If we apply this Fourier transform to a state of the form
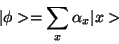 |
(13) |
we get for the Quantum Fourier Transform
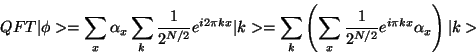 |
(14) |
The term in the brackets is just the discrete Fourier transform of 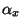 .
.
Note again that the representation 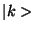 is the bit reversed of the
representation of
is the bit reversed of the
representation of 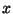 . While one could do a bit reversal operation to get
. While one could do a bit reversal operation to get 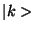 into the same bit order as
into the same bit order as 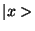 , there is no point.
, there is no point.


Next: Factoring
Up: Quantum Computing Notes
Previous: Quantum Computing Notes
Bill Unruh
2000-03-15
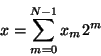
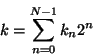
![]() is
is
![]() , namely
, namely ![]() . Let me assume that we have managed to
transform the state
. Let me assume that we have managed to
transform the state ![]() by replacing the
by replacing the ![]() highest digits of
highest digits of ![]() with the
lowest
with the
lowest ![]() digits of
digits of ![]() . I.e., I have created, by some sequence of
transformations, the state
. I.e., I have created, by some sequence of
transformations, the state
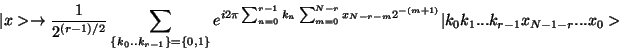
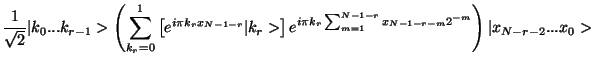
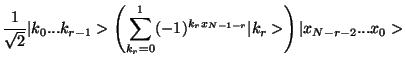
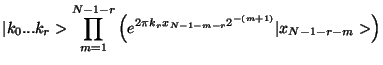
![]() bits, it requires a single
bits, it requires a single ![]() rotation of a single bit, and
rotation of a single bit, and ![]() controlled single-bit phase
rotations, for a total of
controlled single-bit phase
rotations, for a total of ![]() operations.
Thus the whole Fourier transformation requires
operations.
Thus the whole Fourier transformation requires
![]() operations
(
operations
(![]() , we recall is the number of bits in each of the numbers).
, we recall is the number of bits in each of the numbers).
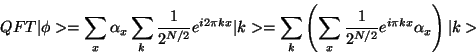
![]() is the bit reversed of the
representation of
is the bit reversed of the
representation of ![]() . While one could do a bit reversal operation to get
. While one could do a bit reversal operation to get ![]() into the same bit order as
into the same bit order as ![]() , there is no point.
, there is no point.