The way he solved this problem was to assume that the planet went around the earth, in the first approximation along a circle. However, that motion was not the end of the motion. The point on the circle (called the defereent) was an empty point-- ie there was nothing there. It however formed the center for another circle that the plant actually travelled on. This circle was the epicycle. He found that in order to get the best fit to the motion of the planet, the line from the center of the epicycle on the deferent to the location of the planet itself on the epicycle must be parallel to the line connecting the earth to the "mean sun"-- ie the location of a virtual sun along the ecliptic (the sun's orbit) which travels uniformly along the ecliptic. It, it starts and ends the year were the true sun does, but it moves with a uniform angular velocity along the ecliptic.
The motion of the planet around the epicycle thus occurs at the rate of one revolution in one year. The center of the epicycle on the deferent on the other hand completes one rotation in a time typical for the planet. (1.5 years for Mars, etc). Because of the outer planets, the earth year is much shorter than the planet's "year" the velocity around the epicycle is greater than the velocity of the deferent point around the deferent. When the plane it outside the deferent, its velocity is in generally the same direction as the deferent velocity and adds to the deferent velocity to give the planet's valocity. When the planet is inside the deferent, the velocity around the epicycle subtracts fromt eh deferent velocity, and for all the outer planets, that subtraction produces a net negative velocity for the planet, giving the retrograde motion.
[ If the video does not work, try Orbit0.gif]
The other feature is that while the epicycle lies in the plane parallel to the orbit of the sun (the ecliptic) the deferent does not, but lies in a plane through the earth tilted slightly to the ecliptic. (Except for Mercury, the tilt of the plane is less than 4 degrees so the deferent circle lies almost parallel to the ecliptic. In the movie above this tilt is taken to be .1 radian or about 6 degrees for clarity. It is this tilt which leads to the loops and S shapes of the retrograde motion of the planets instead of the planet just backtracking exactly its original orbit.
[ If the video does not work, try Orbit90.gif]
This shows the same situation as the previous video only this time looking at the system from 90 degrees from the side. You can see the slope of the blue with respect to the red and the green circles. This is the angle that the planet's orbit makes with the ecliptic. You can also so the retrogressive portions of the orbit where the planet seems to go backwards.
See also http://www.polaris.iastate.edu/EveningStar/Unit2/unit2_sub1.htm a module from Iowa State Univ.
Ptolemy altered this stucture both for the sun and for the planets. He had the circle on which the planet or the sun travelled by centered away from the earth. But this center of the circle was not the point around which the motion of the planet or the sun was uniform (ie equal angles in equal time). That instead was around a point which was equally far from the center of the circle as the earth was but on the other side of the center. That point was called the equant. For the sun, the equant was located at the same point as the center of Hypparchoses orbit, but in Ptolemy's system the center of the circle was placed half way between this point and the earth.
[ If the video does not work, try equant.gif]
In this movie the distance between the earth and the equant is grossly exagerated so that this distance is about .3 of the diameter of the deferent. The maximum for any panet (Mercury) is about .2, with the earth's (sun's in Ptolemey's system) is about .016. This ratio is called the eccentricity.
For the planets this was the structure of the deferent. For each planet there was an equant and a center of the deferent circle, which lay half way between the equant and the center of the earth. There was nothing physical located at the either the center of the circle or at the equant. But these vacant points, plus the vacant point on the deferent that was the center of the epicycle, were crucial for the behaviour of the planet in its orbit. Ptolemy had stretched the the key features of the theoretical model (uniform motion on circles) almost to their breaking point, but felt compelled to do so by the data. As we will see with Kepler, it was precisely these features which turned out to crucial in the new model which Kepler introduced for the planetary orbits, and which we still retain in our current theory of the orbits.
He did not choose the epicycle to have this equant structure to its behaviour,
but both the center, and the point of uniform angular motion of the epicycle
were at the same point (he assumed a zero eccentricity for the orbit of the
epicycle). This meant that the line from the center of the
epicycle to the planet could not be parallel to the line from the earth to the
true sun, because the true sun does not rotate uniformly about the center of
its orbit. Instead it was parallel to
the line from the earth to the mean sun, which does revolve uniformly around
the earth. (Had we lived on Venus, whose orbital eccentricity now is .007, the
approximation he made would have extremely good, instead of only very very
good)

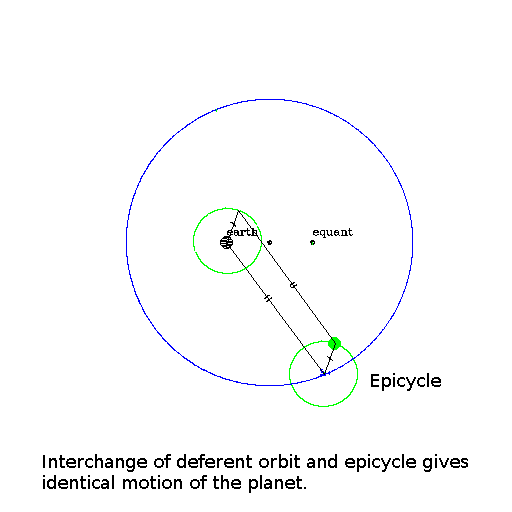
One of the features of the double orbit structure is that it does not matter if one swaps the epicycle and the deferent. Ie, if we center the epicycle at the earth, place the earth's location in the deferent at the location of on the planet on the epicycle, and the epicycle's location on the epicycle by the planet, the motion of the planet will be identical no matter which way you take the geometry. The lines from the earth to the vacant points in the two cases, and then to the planet form a parallelogram, in which the opposite sides have the same lengths and angles, which mean that the planet's relation with the earth remains the same.
[ If the video does not work, try Orbitrev0-.gif]
This exactly the same situation as movie above of the planet on the epicycle circling on the deferent, except here it is the planet on the old deferent circling on the old the epicycle Notice doing it this way how suggestive it is to just scale up the green circle so it lies on the red circle. Ie, the planet on the old scaled deferent circles the sun.
One of the features of the Ptolemeic system was that only angles with their vertex at the earth were measureable. This meant that one could arbitrarly alter the scale, the size of the whole orbital structure for each of the planets. One could make the deferent huge or small, and it would make no difference to the planets. The only limit was the parallax that one could meaure by looking at the planets from different locations on the earth. This was how Hipparchos measured the distance to the moon, by loooking at the parallax of the moon during a solar eclipse from different locations on the earth (eg, the Hellespont (Dardenelles) where the eclipse was total, and at Alexandria where the maximum excursion of the moon over the sun was measured. Since both the moon and sun have the same angular size of about 30 min of arc, this allowed him to determine how far the moon's location moved just becuase of the different locations on the earth.
Unfortuately the parallax of the planets if one travels over the earth is far too small to be observable by the naked eye. Using telescopes observing Venus as it transits the sun, one could play the same game as Hipparchus did to the moon, to determine its distance from the earth. However that was not possible until the 17th century after the invention of the telescope. And was finally done in the 18th century. The main purpose of one of Captian Cook's voyages was to time the transit of Venus across the face of the sun to determine the parallax of Venus between Taihiti and London, and to accurately determine the distance to Venus, and thus to the Sun. (The ratio of Venus' orbit and the earth/sun orbit was already determined by Ptolemy).
In order to pack the planets as tightly as possible without any orbits
crossing those of another planet, Ptolemy chose the inner
planets so that the epicycle was smaller than the deferent as well. This made
the deferent the circle where the point of orbit of the epicycle is in the
same direction from the earth as the mean sun. The epicycle for the inner
planet has arbitrary
phase and circles the epicycle in one of the planet's years. Ie,for the outer
planets, the epicycle circles on the deferent in one planet year, while the
planet circles on the epicycle in one earth year. For the inner planet the
epicycle circles on the deferent in one earth year, while the planet circles
on the epicycle in one planet year.
He carefully arranged all of the planets so that none of their orbits crossed
each other. This was because he still believed in Aristotle's "crystal
spheres". Aristotle believed that the planets, the sun, the stars and moon
were all carried along on crystal spheres (crystal in this case simply meaning
transparent.) Of course with the epicycles he would have had to have holes in
the spheres so that the epicycles could get through, but those holes are at
fixed places on the deferent spheres. He could not have any one planet
crossing through any other planet's spheres or the planet would run into the
sphere, shattering it!
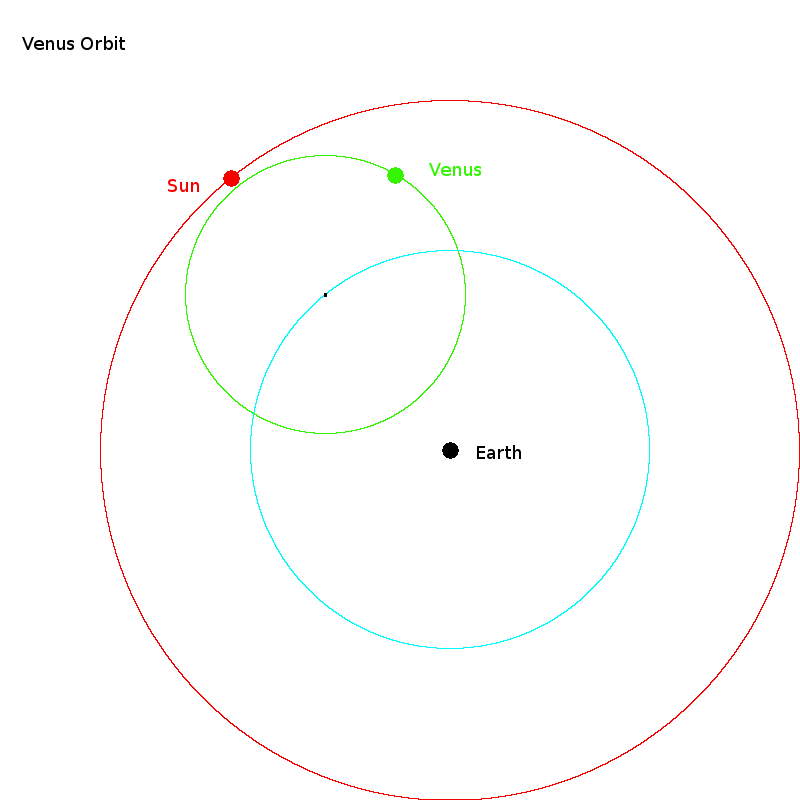
This would be one possibility for Venus' orbit. It would agree with the brighting of Venus, as it comes close to the earth. It would disagree with the parallax-- since Venus here is closer to the earth than the sun, and since Aristachus' estimate for the distance to the sun was also close to Hipparchus' value if the parallax of the sun was just unmeasureable, this would make Venus close enough that meaurements of its paralax should be larger than measureable.
On the other hand if one put Venus outside the sun's orbit, its parallax would definitely be unmeasureable, but the brightning of venus in different parts of its orbit would not be enough to account for what we see. Accounting for the brightening of the planets was one of the weaknesses of the Ptolemeic model.
If one rescaled all of the orbits to make the epicycle(outer planets)/deferent(inner) , one got another present. The ratio of the epicycle to the deferent is fixed by the size of the non-uniform, retrograde motions of the planet. One cannot change that ratio. But if one now believes one knows that the epicycle must be the same size as the solar orbit for each planet, one then also knows the scale fo the deferent for each plant. One then has the relative size of each orbit of each planet in the solar system in comparison to the solar/earth orbit. One knows what the ordering of the planets it. After this rescaling the distance from the sun to Saturn was over 9 times the distance of the earth from the sun, very similar to the distance to Saturn with Ptolemy's close packing. However the stars would have to be at least 800 times the earth orbit away (assuming that one could measure parallax to 10 min of arc. If one measured to 1 min of arc, as Brahe could do, the stars would have to be about 8000 times the distance from the earth to the sun.
One could simply accept that all of the planets orbit the sun, and the sun orbits the earth. Or one could make a leap (after all the size of the sun is almost certainly much large than the earth-- the minimum size that Hypparchus found, on the assumption that the sun was far enough away that one could not see any parallax of the sun as one travelled over the earth would make the sun at least 20 times larger than the earth.) Surely the small should orbit the large, not vice versa. The choice was arbitrary. And Copernicus chose that the earth also orbits the sun. He may also have felt that the sun was a far more fitting object to be at the center, since the earth was the location of so much decay and dirt and corruption that it did not deserve a central position. The important point is that his decision was not a decision based on observation or reason. It was a gut instinct.
Tycho Brahe, the foremost observational astronomer of the day, chose the other. Everything orbits the sun, except that the sun obits the earth. And the reason was scientific, not philosophical. If the earth orbits the sun, then the earth moves a huge distance over the course of a year-- at least twice the distance from the earth to the sun. This large movement would create a parallax for anything else one looked at. Now, the epicycles in Ptolemy's model could simply be looked on as the effect of this parallax on the apparent position of the planets. As the earth moves faster around the sun than the planet, the angle would change, and would change rapidly enough that the planet could seem to be moving backwards. (If one passes another car on the road, the parallax can make it seem as though that car is moving backwards when compared with the distant scenery).
However, one should be able to see parallax for the distant stars as well. And no such parallax had ever been seen. Brahe had developed his observational techniques that he could have seen a parallax of the order of a minute of arc -- about 1/200th of a radian, and he had never seen any parallax for the stars. So one would either have to say that there was none-- ie the earth did not move-- or that the stars were so distant that no parallax would have been visible. Ie, the stars must be about a thousand times further away than even Saturn is. That seemed to him to be unlikely. In fact he felt that he could see that some stars are bigger than others. To do so at that distance would mean that the stars would have to be larger than the distance from the sun to the earth. [He was fooled by a feature of the eye that bright spots of light seem bigger than dim ones. Light scatter from one cone in the eye to neighbouring ones] (It actually took until the 1800s for the parallax of some stars to be seen and is less than 1 second of arc even for the nearest stars). It was only after Newton developed his theory of gravitation that the Copernican choice became the rational choice.
Copernicus paid a heavy price for his beliefs that circular motion, uniform about the center of the circle, must be the only type of motion allowed in the heavens. Ptolemy had introduced the equant for a reason, to accurately descibe the motion of the heavens. Copernicus had to reintroduce new epicycles to account for the deviations of the motion from uniform that Ptolemy had explained. Thus while he removed one epicycle from each planet, he was forced to introduce more than one to describe what Ptolemy had done without epicycles in his theory. Copernicus's theory was a far worse kludge than was Ptolemy's. But one could not take away from him his astonishing accomplishment of having both explained Ptolemy's epicycles, and having ordered the planets.
He could have accepted the equant structure, and hypothosised that the Ptolemy's epicycles should have had the same equant structure as did the sun, that the epicycles themselves had a more complex structure than Ptolemy had given them. This would have been a perfectly acceptable structure. It also would have made Kepler's job much more difficult, because the, with the approriate equants, the Copernican structure of the heavens would have been in far better agreement with the heavens than Copernicus had for his model.
Note that it is simply a lie that Ptolemy's structure suffered from a problem of multiplying epicycles. As the image of in the heavens of the earth's orbit around the sun, the epicycles he had are a necessity if one is to describe the heavens as seen from the moving earth. It was Copernicus' theory that suffered from multiplying epicycles.
One of the real mysteries was why Ptolemy did not come up with Copernicus' model. He had created the key results-- the epicycles for the planets that one could sometimes see even at midnight, and the deferents for the "inner planets" always stuck close to the sun. He could have rescaled the orbits so all of those were the same size as the sun's orbit and come up with Brahe's model. Why didn't he? Did Aristotle's crystal spheres play too strong a role in his mind? Did he just get tired having accomplished so much? That it took European science 1300 years to see the possibility is not surprizing given the intellectual state of Europe after the fall of the Roman Empire. But the strong Islamic tradition in science for the 700 years from the foundation of Islam to the Reconquista could have seen the possibility and apparently did not.
copyright W Unruh (2018)