
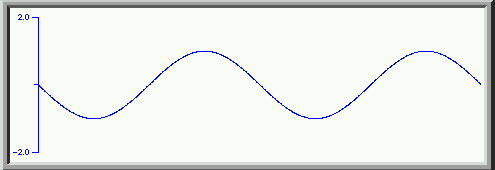
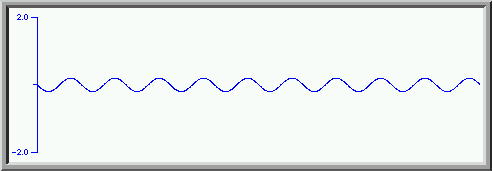
We start with the fundamental with unit amplitude.
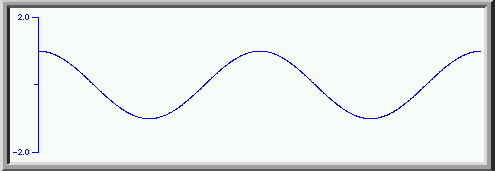
We add to this the third harmonic ( taking the definition of the first harmonic to be the same as the fundamental-- a practice endorsed by the text but at variance with most music terminology) with 1/3 amplitude and with a phase shift of 180 degrees.
to get this. Note that this addition has flattened out the tops and bottoms and increased the slope as the wave passes through zero.
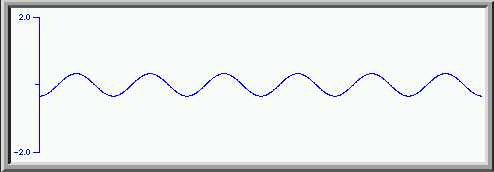
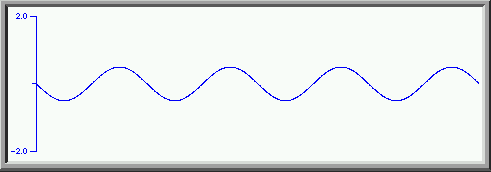
We now add some of the fifth harmonic with amplitude 1/5
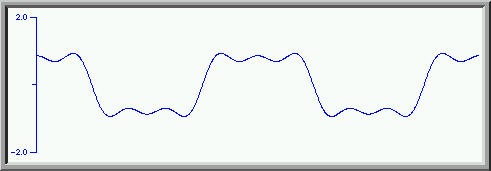
to get this. A closer approximation to the square wave. The top is flatter, and the sides are more nearly vertical.
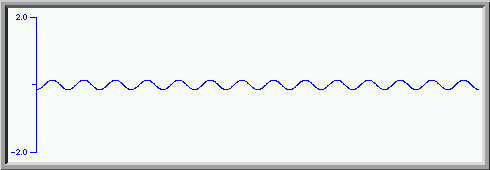
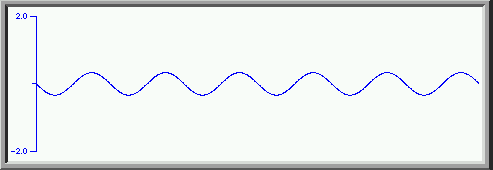
Adding the seventh harmonic, again with an amplitude of 1/7 and a phase of 180degrees.
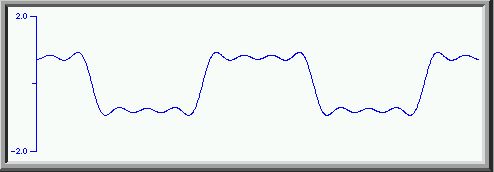
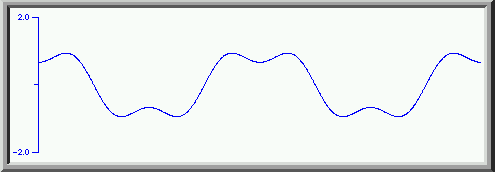
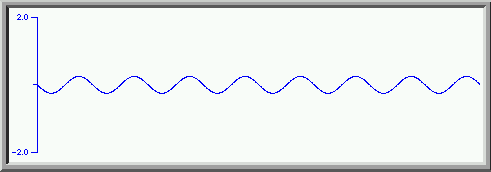
We get an even better approximation to a square wave. We can continue this process with higher and higher harmonics coming closer and closer to a square wave. Adding the first thirty harmonics ( the odd ones each with amplitude of one over the harmonic number and each second odd harmonic with a phase shift of 180 degrees) we get
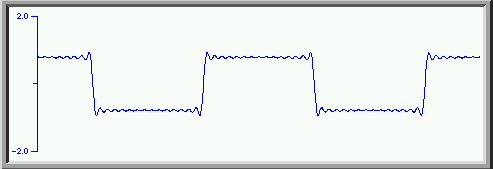
a much closer approximation to the square wave. The "ringing" ( the wiggles near the vertical parts of the square wave) are a consequence of trying to approximate a vertical line ( a "discontinuity") with a sum of sinusoidal waves.
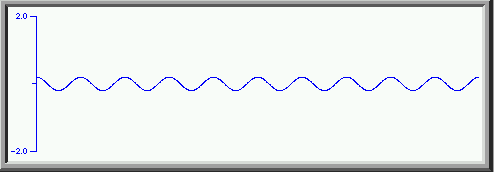
Adding the first 5 components gives us
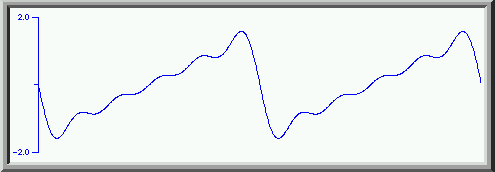
which is a reasonable approximation to a sawtooth wave. Adding even more harmonics, again up to the thirtieth gives us
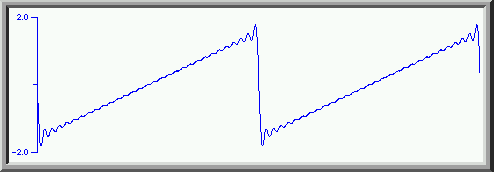
Again, because of the vertical line, we get ringing in the wave near that vertical line.
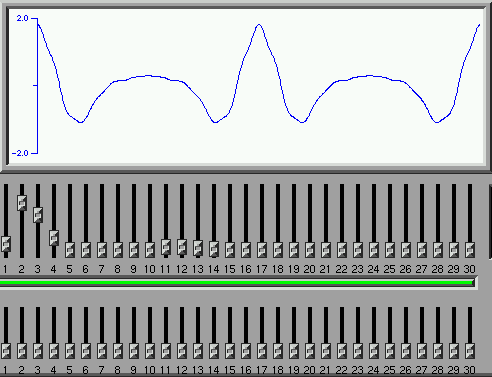
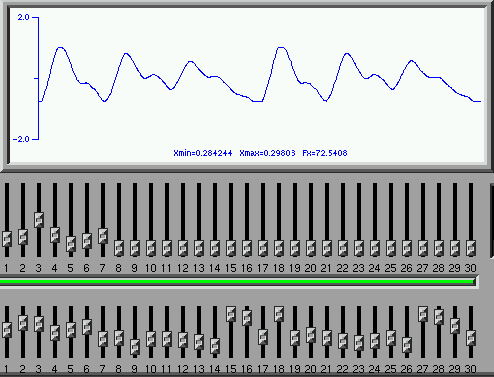
Note the strong third harmonic, and the secondary peak around the seventh harmonic in the amplitude of the various components. These "peaks" in the amplitude are called formants in the voice and arise due to resonances of the air tract between the larynx and the mouth.